Exercícios De Função Do Segundo Grau Com Gabarito – Beduka: Embarque numa jornada fascinante pelo universo das funções quadráticas! Prepare-se para desvendar os mistérios por trás dessas equações, dominando técnicas eficazes de resolução e aplicando seus conhecimentos em situações reais. De problemas de física a desafios econômicos, as funções do segundo grau revelam-se ferramentas poderosas para modelar o mundo ao nosso redor.
Nesta exploração, descobriremos diferentes tipos de exercícios, desde os mais simples aos mais complexos, aprimorando nossas habilidades e construindo uma base sólida para o sucesso.
Aprenderemos a identificar e superar os erros mais comuns, explorando métodos como Bhaskara, soma e produto, e fatoração. A interpretação geométrica, com o auxílio de gráficos e tabelas, será fundamental para visualizar e compreender o comportamento dessas funções. Com o gabarito Beduka como guia, verificaremos nossos resultados, consolidando nosso aprendizado e construindo confiança em cada passo da jornada.
Prepare-se para transformar desafios em conquistas e dominar as funções do segundo grau de forma definitiva!
Recursos e Estratégias de Resolução: Exercícios De Função Do Segundo Grau Com Gabarito – Beduka

A jornada pela compreensão das funções do segundo grau se revela ainda mais rica quando desvendamos as ferramentas e estratégias que nos permitem decifrar seus segredos. Dominar esses métodos não apenas garante a resolução eficiente de problemas, mas também proporciona uma visão mais profunda da natureza dessas funções e de seu comportamento gráfico. Prepare-se para embarcar nessa aventura matemática, equipando-se com as chaves para desvendar os enigmas das parábolas.
Métodos para Encontrar as Raízes de uma Função do Segundo Grau

A busca pelas raízes, ou zeros, de uma função do segundo grau, representa o ponto de partida para uma análise completa. Elas indicam os pontos onde o gráfico intercepta o eixo x, fornecendo informações cruciais sobre o comportamento da função. Existem diversos caminhos para alcançar esse objetivo, cada um com sua elegância e aplicabilidade.
- Fórmula de Bhaskara: Uma ferramenta poderosa e universal, a fórmula de Bhaskara nos fornece as raízes (x) de uma equação do segundo grau na forma ax² + bx + c = 0, através da expressão:
x = (-b ± √(b²
-4ac)) / 2a. Sua aplicação é direta, independente da natureza das raízes (reais e distintas, reais e iguais ou complexas).
- Soma e Produto das Raízes: Para equações do segundo grau com raízes reais, este método se mostra elegante e eficiente. Sabendo que a soma das raízes (x₁ + x₂) é igual a -b/a e o produto das raízes (x₁
– x₂) é igual a c/a, podemos, a partir dessas relações, encontrar as raízes. Este método é particularmente útil quando as raízes são números inteiros ou frações simples. - Fatoração: A fatoração consiste em reescrever a equação do segundo grau como um produto de dois fatores lineares. Por exemplo, a equação x²
-5x + 6 = 0 pode ser fatorada como (x – 2)(x – 3) = 0, resultando nas raízes x₁ = 2 e x₂ = 3. Este método é eficiente quando a fatoração é facilmente identificável.
Determinação do Vértice de uma Parábola e sua Importância, Exercícios De Função Do Segundo Grau Com Gabarito – Beduka
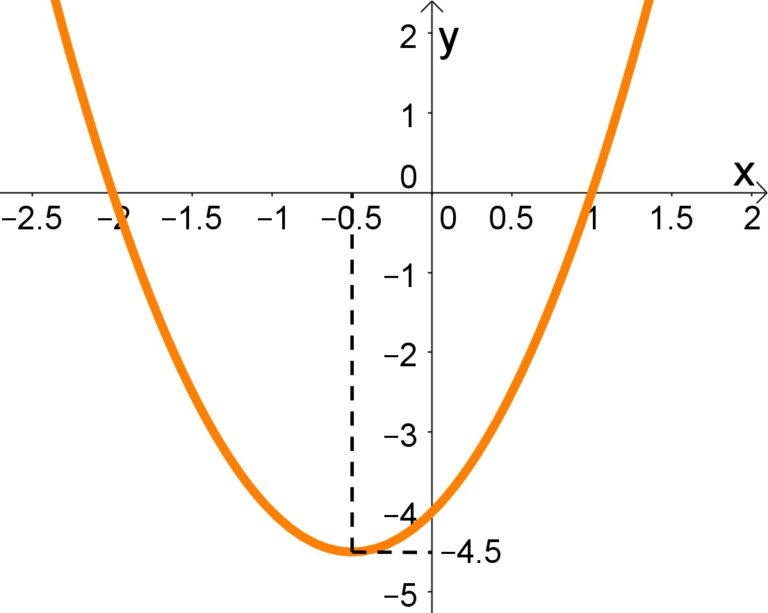
O vértice da parábola, ponto de máximo ou mínimo da função, desempenha um papel central na análise da função do segundo grau. Ele representa o ponto de inflexão da curva, definindo a simetria da parábola e fornecendo informações cruciais sobre o valor máximo ou mínimo da função. As coordenadas do vértice (xv, yv) podem ser determinadas pelas fórmulas:
xv = -b/2a
e
yv = -Δ/4a
, onde Δ = b²4ac (o discriminante). A importância do vértice reside na sua capacidade de fornecer informações sobre o comportamento da função, como seu valor máximo ou mínimo e o eixo de simetria.
Construção do Gráfico de uma Função do Segundo Grau
A construção do gráfico de uma função do segundo grau, a parábola, é um processo visual que consolida o entendimento da função. Para construir o gráfico, podemos seguir estes passos:
- Determinar as raízes da função utilizando um dos métodos apresentados anteriormente.
- Calcular as coordenadas do vértice da parábola.
- Determinar o ponto de interseção com o eixo y (y = c).
- Traçar os pontos encontrados em um plano cartesiano e conectar os pontos para formar a parábola, lembrando que a parábola é simétrica em relação ao eixo vertical que passa pelo vértice.
Utilização do Gabarito do Beduka para Verificação de Resolução

O gabarito do Beduka funciona como um guia precioso na verificação de nossos cálculos e na identificação de possíveis erros. Ele nos permite confrontar nossas respostas com as soluções corretas, oferecendo a oportunidade de revisão e aprimoramento do nosso raciocínio.Vamos ilustrar com um exemplo: Exercício: Encontre as raízes da função f(x) = 2x² – 5x + 2. Resolução:
- Método escolhido: Fórmula de Bhaskara.
- Identificação dos coeficientes: a = 2, b = -5, c = 2.
- Aplicação da fórmula: x = (5 ± √((-5)²
-4
– 2
– 2)) / (2
– 2) = (5 ± √9) / 4 = (5 ± 3) / 4 - Cálculo das raízes: x₁ = (5 + 3) / 4 = 2 e x₂ = (5 – 3) / 4 = 1/2
- Verificação no gabarito do Beduka: Comparando nossas raízes (2 e 1/2) com as do gabarito, podemos confirmar a correção da nossa resolução. Caso haja discrepância, podemos rever cada passo do processo para identificar o erro.

