Exemplos De Medidas De Tendência Central são ferramentas essenciais na análise de dados, fornecendo uma visão geral da distribuição de um conjunto de valores. A média, a mediana e a moda são medidas de tendência central que representam diferentes aspectos da centralidade dos dados.
Compreender as características e aplicações de cada medida permite uma análise mais completa e precisa, revelando padrões e tendências importantes em conjuntos de dados.
Este artigo explora a importância das medidas de tendência central, detalhando os métodos de cálculo e interpretação para cada uma delas. Através de exemplos práticos, você aprenderá a aplicar esses conceitos em cenários reais, compreendendo como cada medida fornece insights distintos sobre a natureza dos dados.
A comparação entre as medidas, seus pontos fortes e fracos, é fundamental para a escolha da ferramenta mais adequada para cada análise.
Introdução às Medidas de Tendência Central
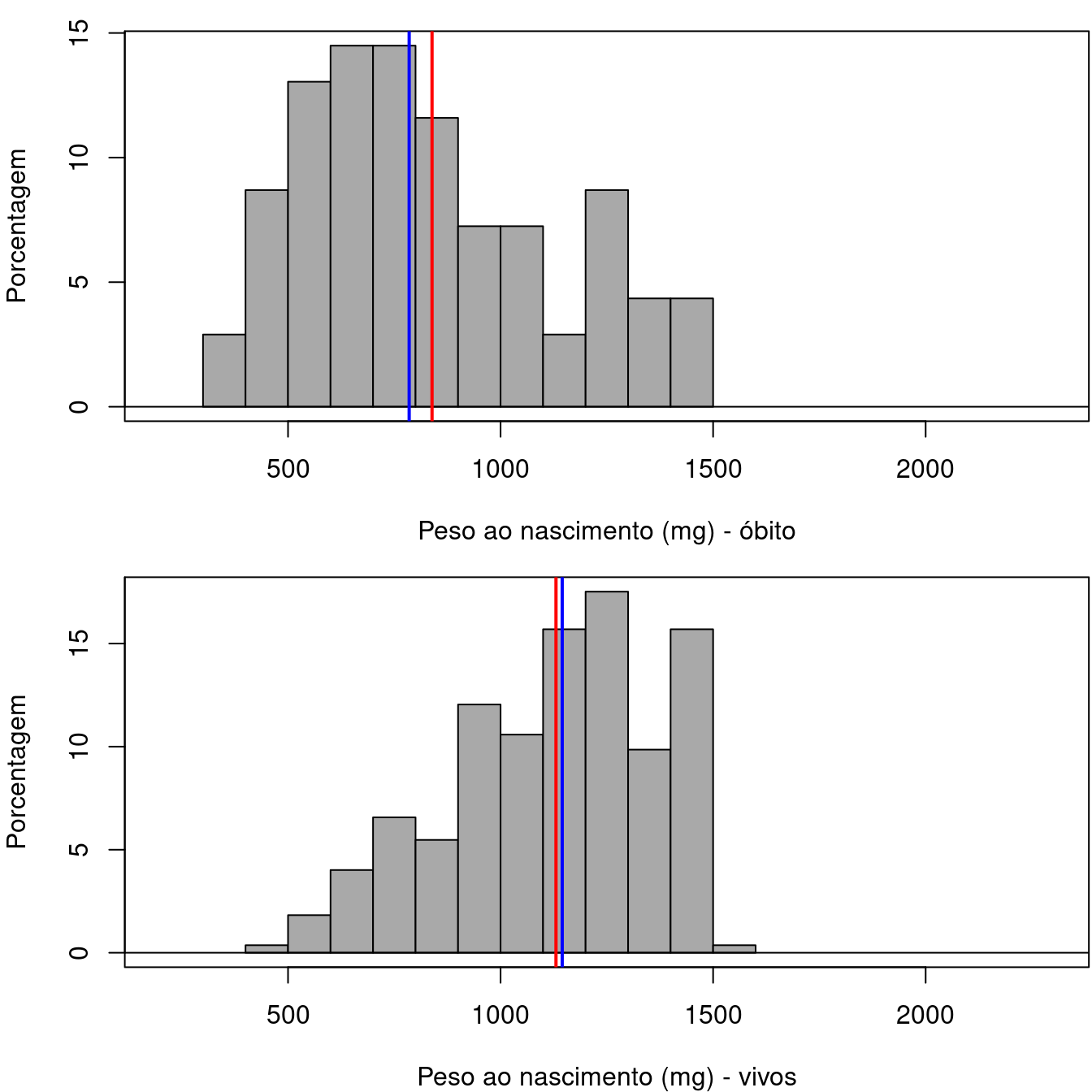
As medidas de tendência central são ferramentas estatísticas cruciais para resumir e interpretar conjuntos de dados. Elas fornecem um valor representativo que indica o centro ou a localização típica dos dados, permitindo uma compreensão rápida e eficiente das características principais de um conjunto de dados.
Essas medidas são amplamente utilizadas em diversas áreas, como negócios, saúde, engenharia e pesquisa, para análise de dados, tomada de decisões e comunicação de informações.
Tipos de Medidas de Tendência Central
Existem três medidas de tendência central comumente utilizadas: média, mediana e moda.
- Média: A média aritmética é a soma de todos os valores de um conjunto de dados dividida pelo número total de valores. É a medida de tendência central mais comum e representa o valor médio dos dados. A média é sensível a valores extremos, o que significa que valores muito altos ou muito baixos podem distorcer a média.
- Mediana: A mediana é o valor do meio em um conjunto de dados ordenado. Ela divide o conjunto de dados em duas metades, com metade dos valores acima da mediana e a outra metade abaixo. A mediana é menos sensível a valores extremos do que a média e é uma medida mais robusta para dados com outliers.
- Moda: A moda é o valor que ocorre com mais frequência em um conjunto de dados. É a medida de tendência central mais adequada para dados categóricos ou dados com valores repetidos. A moda pode não ser única, ou seja, pode haver vários valores com a mesma frequência máxima.
Comparação das Medidas de Tendência Central
A escolha da medida de tendência central apropriada depende da natureza dos dados e do objetivo da análise. A tabela a seguir compara as características das três medidas de tendência central:
| Medida | Descrição | Pontos Fortes | Pontos Fracos |
|---|---|---|---|
| Média | Soma de todos os valores dividida pelo número total de valores. | Fácil de calcular; considera todos os valores do conjunto de dados. | Sensível a valores extremos; pode ser distorcida por outliers. |
| Mediana | Valor do meio em um conjunto de dados ordenado. | Menos sensível a valores extremos do que a média; representa o ponto médio do conjunto de dados. | Pode não ser representativa para conjuntos de dados pequenos ou com muitos valores repetidos. |
| Moda | Valor que ocorre com mais frequência em um conjunto de dados. | Útil para dados categóricos; identifica o valor mais popular. | Pode não ser única; pode não ser representativa para conjuntos de dados com poucos valores repetidos. |
Cálculo e Interpretação das Medidas de Tendência Central

As medidas de tendência central são ferramentas estatísticas essenciais para resumir e analisar conjuntos de dados. Elas fornecem um único valor que representa o centro ou a tendência geral dos dados. As três medidas de tendência central mais comuns são a média, a mediana e a moda.
Este tópico explorará o cálculo e a interpretação dessas medidas em diferentes cenários.
Cálculo da Média, Mediana e Moda
O cálculo da média, mediana e moda envolve etapas distintas, que são descritas a seguir:
- Média:A média é a soma de todos os valores em um conjunto de dados dividida pelo número total de valores.
Média = (Soma de todos os valores) / (Número total de valores)
- Mediana:A mediana é o valor do meio em um conjunto de dados ordenado. Se o número de valores for par, a mediana é a média dos dois valores do meio.
- Moda:A moda é o valor que aparece com mais frequência em um conjunto de dados. Um conjunto de dados pode ter mais de uma moda, ou pode não ter nenhuma moda.
Interpretação das Medidas de Tendência Central
A interpretação das medidas de tendência central depende do contexto do conjunto de dados e do objetivo da análise.
- Média:A média é uma medida útil para resumir conjuntos de dados simétricos. No entanto, a média pode ser influenciada por valores extremos, ou outliers.
- Mediana:A mediana é uma medida robusta que não é afetada por valores extremos. Ela é uma medida útil para resumir conjuntos de dados assimétricos ou que contêm outliers.
- Moda:A moda é uma medida útil para identificar o valor mais popular em um conjunto de dados. Ela é frequentemente usada para analisar dados categóricos.
Exemplos Práticos
Para ilustrar a aplicação e interpretação das medidas de tendência central, considere os seguintes exemplos:
- Exemplo 1:Suponha que um grupo de estudantes fez um teste e suas notas foram: 70, 80, 85, 90, 95, 100.
- Média:(70 + 80 + 85 + 90 + 95 + 100) / 6 = 85
- Mediana:(85 + 90) / 2 = 87.5
- Moda:Não há moda neste conjunto de dados.
- Exemplo 2:Suponha que uma loja de roupas vendeu os seguintes tamanhos de camisas: P, M, G, GG, GG, G, M, P.
- Moda:O tamanho GG é a moda, pois aparece com mais frequência.
Comparação das Medidas de Tendência Central
| Conjunto de Dados | Média | Mediana | Moda |
|---|---|---|---|
| Notas dos Estudantes (Exemplo 1) | 85 | 87.5 | Não há moda |
| Tamanhos de Camisas (Exemplo 2) | – | – | GG |
Aplicações das Medidas de Tendência Central: Exemplos De Medidas De Tendência Central
As medidas de tendência central desempenham um papel crucial na análise de dados, fornecendo informações valiosas sobre a localização típica de um conjunto de dados. Essas medidas são amplamente aplicadas em diversas áreas, como estatística, negócios, saúde e ciências sociais, permitindo uma compreensão mais profunda dos dados e a tomada de decisões mais eficazes.
Aplicações em Estatística
As medidas de tendência central são ferramentas essenciais na estatística descritiva, ajudando a resumir e interpretar conjuntos de dados.
- A médiaé usada para determinar o valor médio de um conjunto de dados, fornecendo uma representação geral do centro dos dados. Por exemplo, a média das notas dos alunos em um teste pode ser usada para avaliar o desempenho geral da turma.
- A medianaé útil para encontrar o ponto médio de um conjunto de dados ordenado, sendo menos suscetível a valores extremos. Por exemplo, a mediana dos salários de uma empresa pode ser usada para determinar o salário típico dos funcionários, independentemente de alguns salários muito altos ou muito baixos.
- A modaé usada para identificar o valor mais frequente em um conjunto de dados, fornecendo informações sobre o valor mais comum. Por exemplo, a moda dos tamanhos de sapatos vendidos em uma loja pode ser usada para determinar o tamanho mais popular.
Aplicações em Negócios
As medidas de tendência central são ferramentas essenciais para a tomada de decisões em negócios, ajudando a analisar dados financeiros, vendas e marketing.
- A médiaé usada para calcular o lucro médio por venda, o custo médio de produção ou o retorno médio sobre o investimento, fornecendo uma visão geral do desempenho financeiro da empresa.
- A medianaé útil para determinar o salário médio dos funcionários, o preço médio de venda de um produto ou o valor médio de um ativo, fornecendo uma representação mais precisa do centro dos dados, especialmente em casos com valores extremos.
- A modaé usada para identificar o produto mais vendido, o cliente mais frequente ou o período de maior demanda, fornecendo informações sobre os produtos, clientes ou períodos mais populares.
Aplicações em Saúde
As medidas de tendência central são usadas na área da saúde para analisar dados de pacientes, como pressão arterial, peso, altura e níveis de glicose no sangue.
- A médiaé usada para determinar a pressão arterial média de um grupo de pacientes, o peso médio de uma população ou o nível médio de glicose no sangue, fornecendo uma visão geral do estado de saúde do grupo.
- A medianaé útil para encontrar o ponto médio da pressão arterial, do peso ou do nível de glicose no sangue, sendo menos suscetível a valores extremos, como casos de pacientes com doenças crônicas.
- A modaé usada para identificar a faixa etária mais comum entre os pacientes com uma determinada doença, o tipo de medicamento mais prescrito ou o sintoma mais comum, fornecendo informações sobre os padrões de saúde.
Aplicações em Ciências Sociais
As medidas de tendência central são amplamente usadas em pesquisas sociais para analisar dados sobre renda, educação, criminalidade e outros indicadores sociais.
- A médiaé usada para determinar a renda média de uma população, o nível médio de escolaridade ou a taxa média de criminalidade, fornecendo uma visão geral dos indicadores sociais.
- A medianaé útil para encontrar o ponto médio da renda, do nível de escolaridade ou da taxa de criminalidade, sendo menos suscetível a valores extremos, como casos de indivíduos com rendas muito altas ou muito baixas.
- A modaé usada para identificar o nível de escolaridade mais comum, o grupo étnico mais prevalente ou o tipo de crime mais frequente, fornecendo informações sobre os padrões sociais.
Estudo de Caso: Análise de Dados de Vendas
| Produto | Vendas (Unidades) | Média | Mediana | Moda |
|---|---|---|---|---|
| A | 100, 120, 150, 180, 200 | 150 | 150 | 150 |
| B | 50, 60, 70, 80, 90 | 70 | 70 | 70 |
| C | 20, 30, 40, 50, 60 | 40 | 40 | 40 |
Neste estudo de caso, as medidas de tendência central são usadas para analisar as vendas de três produtos diferentes. A média, mediana e moda das vendas de cada produto são calculadas para fornecer uma visão geral do desempenho de cada produto.
Os resultados mostram que o produto A teve as maiores vendas, seguido pelo produto B e pelo produto C. As medidas de tendência central fornecem informações valiosas sobre o desempenho de cada produto, permitindo que os gestores tomem decisões estratégicas sobre a produção, marketing e vendas de cada produto.
As medidas de tendência central desempenham um papel fundamental na análise de dados, oferecendo uma visão resumida e significativa sobre a distribuição dos valores. A escolha da medida mais apropriada depende do contexto e do objetivo da análise, com cada medida revelando aspectos específicos da centralidade dos dados.
Ao dominar o cálculo e a interpretação dessas medidas, você estará equipado para analisar dados de forma mais eficiente e extrair insights relevantes para a tomada de decisões informadas.

